Perimeter and Area Formulas for two dimensional geometrical figures

In this page provided formulas of Perimeter and Area for two dimensional geometrical figures like square, rectangle, Rhombus, parallelogram, trapezium or trapezoid, triangle, right angle triangle, ellipse, circle, sector of a circle, segment of a circle etc

Formulas for Two Dimensional Geometrical Figures

Square

Side for square = a & Length of diagonal = d

Area of the square = A = side² = a² = (1/2) d²

Perimeter of the square = P = 4 × side = 4 a

Length of diagonal = d = $a \sqrt{2} \ = \ \sqrt{2 \times \ A } = \ \frac{P}{4} \sqrt{2}$

Rectangle

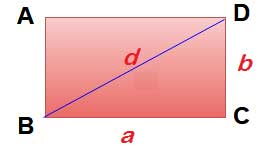Perimeter of the rectangle = 2 × (length + width) = 2 (a + b)

Area of the rectangle = length × width = ab

Length of diagonal ( d ) = √ (a² + b²)

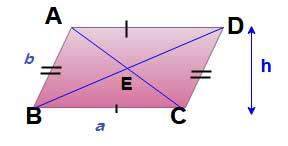
Rhombus

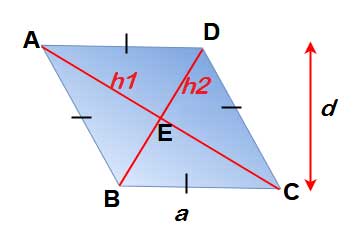For Rhombus all sides are equal = a, Vertical Height = d & h1, h2 are the diagonals also AB || DC , AD || BC

Perimeter of rhombus = 4a

Area of the Rhombus = ad = (1/2) d1 d2

Parallelogram

Area of parallelogram = base × height = a x h

Perimeter of parallelogram = 2 × (side1 + side2) = 2 ( a + b)

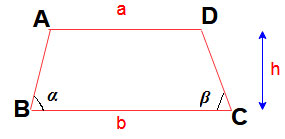
Trapezium (Trapezoid)

In trapezium two sides are in parallel,

Area of Trapezium or Trapezoid = $\frac{1}{2} \ (a+b)h$

Perimeter of Trapezium or Trapezoid = $a + b + h \left [ \frac{1}{sin\alpha} + \frac{1}{sin \beta} \right ]$

Triangle

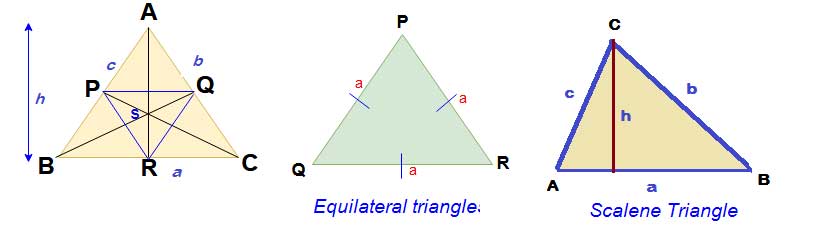Formulas for triangle

Area of the triangle = (1/2) x Base x Height = $\frac{ 1 }{2} \times \ a \times \ h$

Area of the triangle = $\sqrt{S(S-a)(S-b)(S-c)}$

Where Semi perimeter = $S = \frac{a+b+c}{2}$

Radius of incircle triangle = Area /S

Formulas for equilateral triangle

Perimeter of the equilateral triangle = 3 x Side = 3a

Area of the equilateral triangle = $\frac{\sqrt{3}}{4} \times (Side )^2$ = 0.433 x (side)²

Radius of circumference circle of an equilateral triangle = $S = \frac{Side \ ^3}{4\times Area \ of \ Triangle}$ = $\frac{a}{\sqrt{3}$

Area of circumference circle of an equilateral triangle = $\pi \times \left ( \frac{a}{\sqrt{3}} \right )^2$

Radius of incircle of an equilateral triangle = $= \frac{ Area \ of \ Triangle}{ Semi \ perimeter (S) }$ = $\frac{a}{2\sqrt{3}$ a / (2 √3)

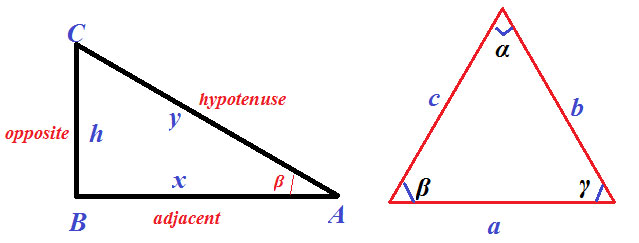
Formulas for Right Angle Triangle & Formula for length of a triangle when given by one side and angle

In above figure ABC is a right angle triangle x = length of adjacent side, y = length of hypotenuse & h = height of the triangle.

Pythagoras’ Law – $x^2 + h^2 = y^2$

Area of the right angle triangle = $\frac{1}{2} xh$

Sin β = h / y ⇒ h = y Sin β

Cos β = x / y ⇒ x = y Cos β

Tan β = h / x ⇒ h = x Tan β

Cosine Law

c² = a² + b² – 2 ab Cos γ

b² = a² + c² – 2 ac Cos β

a² = b2 + c² – 2 bc Cos α

Sine Law $\frac{a}{sin \ \alpha} = \frac{b}{sin \ \beta} = \frac{c}{sin \ \gamma}$

Area of a Triangle

$\frac{b \ c \ sin \ \alpha}{2} = \frac{a \ c \ sin \ \beta}{2} = \frac{a\ b \ sin \ \gamma}{2}$

Circle

Formulas for Area and circumference of the circle

Area of a circle (A ) = π x (Radius) ² = π r ² = ( π/4 ) D² = 0.7854 x D²

Diameter of a circle (D) = $\sqrt { \frac{Area \ of \ a \ circle}{0.7854}}$

Circumference of a circle ( C ) = 2 π x Radius = 2 π r = π D

Area of circle =( 1/2) x Circumference x radius = (1/2) x C x r

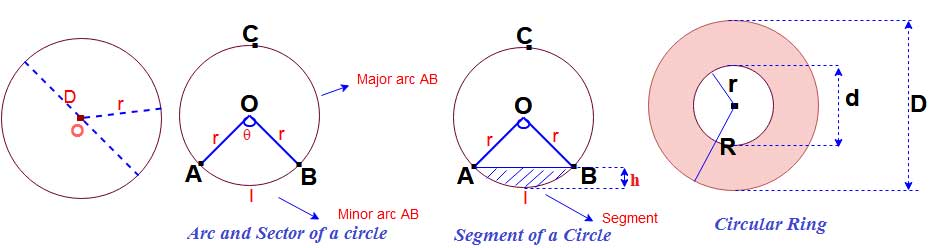
Formula for Arc and sector of a circle

Arc length of circle ( l ) = $\frac{ \theta }{360} \times 2\pi r \ = \ \frac{ \theta \ \pi r }{180}$

Area of the sector (minor) = $\frac{ \theta }{360} \times \pi r^2 \$

If the angle θ is in radians mean one radian = 180/π , then

The area of the sector = $\frac{ \theta }{2} \times r^2 \$

Sector angle of a circle θ = $\frac{ 180 \times l }{\pi r}$

Segment of circle and perimeter of segment

Area of the segment = $\left ( \frac{\theta}{360} \right )\pi r^2 \ -\ \left ( \frac{1}{2} \right ) \ sin\theta \ r^2$

Perimeter of the segment = $\left ( \frac{\theta \ \pi \ r }{180} \right ) \ -\ 2r \ sin\theta \ \left ( \frac{\theta}{2} \right )$

Arc Length of the circle segment = l = 0.01745 x r x θ

Chord length of the circle = $\ 2r \ sin\theta \ \left ( \frac{\theta}{2} \right )$ = $2 \ \sqrt{h (2r -h)}$

Area of the circular ring

Area of a circular ring = = (π/4) ( D ² – d ²) = 0.7854 (D ² – d ²)

Area of a circular ring = π (R ² – r ²)

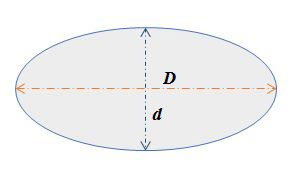
Ellipse

D = Diameter of higher half-axis & d = Diameter of lower half-axis

Area of an Ellipse = $\frac{\pi}{4} \ \times D \times \ d$ = 0.7854 x D x d

D = 2 x radius = 2 m , d = 2 x radius = 2 n

Perimeter of an Ellipse (Formula – 1) ≈ $2\pi \sqrt{ \frac{m^2 \ + \ n^2 }{2} }$

Perimeter of an Ellipse (Formula – 2) ≈ $\pi \ \left [ 3 (m \ + \ n ) - \sqrt{(3m+n) (m+3n)} \right ]$

Both formulas gives approximate values but the formula- 2 gives better approch which is derived by Indian mathematician Ramanujan

Related Articles:

Conversion of units for Engineering Equipment Design & Drawing Calculations

Online Calculator to Find liquid volume for vertically mounted cylindrical having partitioned portion.

Sugar Industry Manufacturing Process Machinery Capacity Calculation

Post Author: siva alluri

The aim of this Blog "sugarprocesstech" is Providing basic to advance knowledge in sugar process industry and providing maximum calculation regarding capacity and equipment design online calculators .

2 thoughts on “Perimeter and Area Formulas for two dimensional geometrical figures”

Pankaj kumar

(November 20, 2022 - 3:43 pm)

Good

siva alluri

(December 2, 2022 - 2:44 pm)

welcome